5장 재귀와 귀납(Recursion and Induction)

아래 주피터 노트북은 James Brock의 learn-you-a-haskell-notebook을 기본틀로 사용합니다.

참고: 린팅(linting) 기능 끄기

  • 린팅(linting): IHaskell에서 HLint라고 불리는 린터(linter)에 의해 보다 적절하다고 판단하는 표현식을 제안하는 기능
  • 보다 세련된 표현식(expression)을 제안하는 도구임. 하지만 반드시 필요한 기능은 아니다
  • 참조: IHaskell의 린팅 기능 설정하기
In [1]:
:opt no-lint

하스켈과 같은 함수형 프로그래밍언어에서는 재귀함수의 역할이 매우 크다. 다른 거의 모든 프로그래밍언어에서도 재귀함수를 지원하지만 그 역할이 상대적으로 미약하다.

여러 이유가 있지만 기본적으로 C, 자바, 파이썬 등의 명령형 프로그래밍언어는 어떻게(how) 메모리를 관리할 것인가에 보다 집중하기 때문이다. 반면에 하스켈은 이것의 정의는 이것이다(is)라는 방식을 사용한다. 더 나아가 하스켈은 재귀함수를 대신하는 역할을 수행하는 while 또는 for 반목문(loop)을 지원하지 아예 않기 때문에 재귀함수의 역할은 매우 크다.

5.1 재귀함수(Recursive Functions)

재귀(recursion)는 함수를 정의하는 과정에서 해당 함수를 다시 활용하는 기법이며 수학에서 자주 활용된다. 예를 들어, 피보나찌(Fibonacci) 수열의 처음 두 값은 0과 1이며, 연속으로 위치한 두 피보나찌 수의 합이 그 다음 피보나찌 수이다. 이 성질을 점화식으로 표현하면 다음과 같다.

fib(0) = 0
fib(1) = 1
fib(n) = fib(n-1) + fib(n-2)

하스켈에서 fib 함수를 아래와 같이 매우 간단하게 재귀함수로 정의할 수 있다.

주의: 하스켈을 포함한 대다수의 프로그래밍언어에서는 0을 자연수로 취급하며, 리스트의 인덱스처럼 0이 첫째 항목을 가리킨다.

In [2]:
fib :: Integer -> Integer
fib 0 = 0
fib 1 = 1
fib n = fib (n-1) + fib (n-2)

위 정의에 의하면, n >= 2 인 경우, fib n을 계산하려면 fib (n-1) 과 fib (n-2) 를 먼저 계산해야 한다. 이와 같이 함수를 정의할 때 해당 함수를 다시 활용하는 방식을 재귀(recursion)라 부른다.

예를 들어, fib(3)이 계산되는 과정은 다음과 같다.

fib 3 = fib 2 + fib 1
      = (fib 1 + fib 0) + fib 1
      = (1 + fib 0) + fib 1
      = (1 + 0) + fib 1
      = 1 + fib 1
      = 1 + 1
      = 2

참고

  • 소괄호를 이용하여 표현된 계산 순서에 주의하라. 예를 들어, 첫째 등호 오른편에 위치한 표현식이 가리키는 값을 계산하기 위해 fib 1의 계산은 fib 2의 계산이 완료될 때까지 기다려야 한다.
  • fib 함수는 음수에 대해서는 계산과정이 절대로 멈추지 않는다.
  • fib 함수가 조금만 커져도 계산과정이 매우 오래 걸릴 수 있다. 실제로 fib n을 계산하는 과정에서 fib 함수의 호출 횟수는 n이 커짐에 따라 기하급수적으로 늘어난다.

시작단계와 재귀단계

fib 3의 계산과정에서 볼 수 있듯이, 0과 1이 시작단계(base case 또는 edge condition)의 역할을 수행하며, 만약 이 시작단계가 없었다면 fib 3의 계산이 절대 끝나지 않을 것이다. 이처럼 재귀함수를 정의할 때 시작단계를 명시하는 일이 매우 중요하다. 반면에 n >= 2 인 경우는 fib 함수를 재귀적으로 호출하는 단계, 즉, 재귀단계(recursive step)라 부른다.

정리하면, 재귀함수를 작성할 때 아래 두 사항을 고려해야 한다.

  • 시작단계: 인자와 반환값을 구체적으로 지정하는 단계
  • 재귀단계: 주어진 인자의 반환값을 지정하는 표현식에 해당 함수가 다시 사용되는 단계

예를 들어, fib 함수의 경우 시작단계와 재귀단계는 다음과 같다.

  • 시작단계: fib 0 = 0 과 fib 1 = 1
  • 재귀단계: fib n = fib (n-1) + fib (n-2)
    • n에 해당하는 피보나찌 수를 지정할 때 fib 함수가 두 번 사용되었음.
    • 주의: 패턴 매칭에 의해 n >= 2가 가정되었음

5.2 구조적 재귀(Structural Recursion)

재귀함수를 정의할 때 사용되는 시작단계와 재귀단계 중에서 재귀단계에 구조적 제약(structural constraints)을 가하는 방식으로 구조적 재귀(structural recursion)를 정의하며, 기본 양식은 다음과 같다.

  • 시작단계: 인자와 반환값을 구체적으로 지정하는 단계
  • 재귀단계: 인자를 특정 패턴으로 지정한 후 해당 패턴의 하위 패턴(subpattern)에 대한 반환값을 활용하는 단계

하위 패턴(subpattern)은 기존의 패턴에 하나의 구성품으로 사용된 패턴을 의미한다. 재귀함수를 구조적 재귀를 이용하여 정의하는 방법을 예제를 통해 살펴본다.

구조적 재귀 예제

예제: maximum 함수 구현

maximum 함수는 크기순으로 정렬될 수 있는 값들로 이루어진 리스트를 인자로 받아 그 중에 가장 큰 값을 반환한다. 따라서, 항목들은 Ord 유형 클래스에 속하는 유형을 가져야 한다. maximum 함수를 재귀로 구현하려면 시작단계와 재귀단계의 경우는 다음과 같이 정할 수 있다.

  • 시작단계:
    • 공리스트인 경우: 반환값 없음. 오류 발생해야 함.
    • 한 개의 항목으로 구성된 리스트의 경우: 주어진 하나의 항목이 최대값임.
  • 재귀단계: 공리스트가 아닌 경우
    • 꼬리(tail)의 최댓값과 머리(head)를 비교하여 큰 값 반환

재귀단계에서 사용되는 '꼬리(tail)의 최댓값'이 바로 구조적 재귀에 해당하며 실제로 구현하면 다음과 같다.

주의: maximum 함수는 이미 정의되어 있기에 여기서는 아포스트로피를 사용하여 새로운 이름으로 정의한다. 이후 소개되는 예제에서도 동일한 방식을 사용하여 기존에 정의된 함수를 재정의한다.

In [3]:
maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty list"
maximum' [x] = x
maximum' (x:xs)
    | x > maxTail = x
    | otherwise = maxTail
    where maxTail = maximum' xs

첫째, 둘째 패턴 매칭은 시작단계에 해당한다. 마지막 셋째 패턴 매칭은 재귀단계이며, 두 개 이상의 항목을 갖는 원소를 나타내기 위해 x:xs를 패턴으로 사용하였다. 위 정의가 구조적 재귀인 이유는 재귀단계의 반환값에 사용된 maximum' 함수의 인자가 xs인데, 이 패턴이 애초에 주어진 x:xs의 하위 패턴이기 때문이다. 실제로 x:xs는 x와 xs라는 두 개의 하위 패턴으로 구성되어 있다.

위 함수에서는 maximum' xs가 가드(guards)와 더불어 where 절에서 maxTail 값을 지정하기 위해 사용되어서 구조적 재귀의 모습이 덜 선명하다. 반면에 max 함수를 이용하는 아래 정의는 구조적 재귀의 활용을 보다 명확하게 보여준다.

In [4]:
maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty list"
maximum' [x] = x
maximum' (x:xs) = max x (maximum' xs)

예를 들어, maximum' [2,5,1]이 재귀적으로 계산되는 과정은 다음과 같다.

maximum' [2,5,1] = max 2 (maximum' [5,1])
                = max 2 (max 5 (maximum' [1]))
                = max 2 (max 5 1)
                = max 2 5
                = 5

참고: 대부분의 명령형 프로그래밍언어는 패턴매칭을 지원하지 않는다. 따라서 재귀함수를 정의할 때 패턴매칭 대신에 많은 if ... else ... 명령문을 사용해야 하거나, 아니면 while 또는 for 반복문을 이용한다. 예를 들어, maximum' 함수의 경우 while 또는 for 반복문을 이용하여 리스트에 포함된 전체 항목을 대상으로 최댓값을 업데이트 하는 방식으로 반환값을 지정할 수 있다.

예제: revese 함수 구현

reverse 함수는 리스트에 포함된 항목들의 순서를 뒤집어서 새로운 리스트를 생성하여 반환한다. 시작단계와 재귀단계는 다음과 같이 지정할 수 있다.

  • 시작단계: 공리스트인 경우이며, 뒤집을 게 전혀 없음.
  • 재귀단계: 머리와 꼬리로 구분하여, 꼬리를 뒤집고, 머리를 오른편 맨 끝에 추가.

하스켈로 구현하면 다음과 같으며, 재귀단계가 구조적 재귀를 사용하였음을 바로 확인할 수 있다.

  • x:xs가 인자 패턴일 때, reverse' xs 가 반환값에 사용되었음.
  • xs는 x:xs의 하위패턴임.
In [5]:
reverse' :: [a] -> [a]
reverse' [] = []
reverse' (x:xs) = reverse' xs ++ [x]
In [6]:
reverse' [1,2,3,4,5]

[5,4,3,2,1]

예제: zip 함수 구현

zip 함수는 두 개의 리스트를 인자로 받아 두 리스트에서 동일한 인덱스를 갖는 값들의 쌍으로 이루어진 리스트를 생성하여 반환한다. 단, 생성된 리스트의 길이는 짧은 리스트의 길이와 동일하다.

예를 들어 zip [1,2,3] ['a','b']의 결과는 다음과 같다.

In [7]:
zip [1,2,3] ['a','b']

[(1,'a'),(2,'b')]

즉, 보다 긴 리스트의 항목 일부는 무시된다.

시작단계는 역시 공리스트를 대상으로 한다. 다만, 인자가 두 개이므로 각각의 인자에 경우를 달리해서 다뤄야 한다. 반면에, 재귀 단계는 두 인자 모두 한 개 이상의 항목을 가질 때이다. zip 함수를 직접 구현하면 다음과 같다.

In [8]:
zip' :: [a] -> [b] -> [(a,b)]
zip' _ [] = []
zip' [] _ = []
zip' (x:xs) (y:ys) = (x,y):zip' xs ys

처음 두 패턴매칭이 시작단계이며, 두 인자 중 하나가 공리스트인 경우를 다룬다. 셋째 패턴매칭은 재귀단계이며, 구조적 재귀를 사용한다.

  • zip' xs ys 에 사용된 두 인자 xs와 ys 각각 x:xs와 y:ys의 하위패턴임.

예를 들어, zip' [1,2,3] ['a','b']이 계산되는 과정은 다음과 같다.

zip' [1,2,3] ['a','b'] = (1,'a') : zip' [2,3] ['b']
                       = (1,'a') : (2,'b') : zip' [3] []
                       = (1,'a') : (2,'b') : []
                       = [(1,'a'),(2,'b')]

아래의 실제 실행결과와 동일하다.

In [10]:
zip' [1,2,3] ['a','b']

[(1,'a'),(2,'b')]

예제: elem 함수 구현

elem 함수는 어떤 값이 어떤 리스트의 항목으로 사용되었는지 여부를 판단하는 함수이다.

  • 시작단계: 공리스트인 경우
  • 재귀단계: 공리스트가 아닌 경우

주의: 리스트의 항목으로 사용되었는지 여부를 판단하려면 항목들의 동치성(equality) 여부를 판단할 수 있어야 한다. 따라서 Eq 유형 클래스에 속하는 유형을 대상으로 elem 함수가 작동한다.

In [11]:
elem' :: (Eq a) => a -> [a] -> Bool
elem' a [] = False
elem' a (x:xs)
    | a == x    = True
    | otherwise = a `elem'` xs

재귀단계에 사용된 elem 함수의 인자는 xs이며, x:xs의 하위패턴이기에 구조적 재귀가 사용된 것이 명확하다.

In [12]:
elem' 3 [1,2,3,4]

True
In [13]:
elem' 5 [1,2,3,4]

False

구조적 재귀의 장점

구조적 재귀의 장점은 사용된 인자의 패턴, 즉 모양에만 의존하여 반환값을 지정한다는 것이다. 즉, 사용된 인자의 의미를 생각할 필요없이 겉모습만 보면 해당 인자의 값을 계산할 수 있다. 실제로 앞서 살펴 본 maximum', reverse', zip', elem' 모두 사용된 인자의 패턴에만 의존한다.

반면에 구조적 재귀가 아닌 경우는 사용되는 인자의 겉모습 뿐만 아니라 의미 또한 반환값을 지정할 때 함께 고려해야 한다. 예를 들어, 두 양의 정수의 최대공약수를 계산하는 유클리드 호제법(Euclidean algorithm)의 경우 구조적 재귀를 사용하지 않는다.

참고: 두 정수의 최대공약수를 계산하는 gcd 함수가 이미 정의되어 있다. 따라서 여기서는 다른 이름을 사용한다.

In [28]:
gcd' :: Integer -> Integer -> Integer
gcd' 0 y = y
gcd' x y = gcd' (y `mod` x) x
In [46]:
gcd' 42 36

6

둘째 패턴, 즉, 0이 아닌 x에 대한 gcd' x y의 계산에 사용된 인자 (y `mod` x)가 x의 하위 패턴이 아니다. 물론, x, y 모두 양의 정수이면 (y `mod` x) 는 x 보다 작은 값이기 때문에 gcd' x y 는 임의의 양의 정수에 대해 항상 최대공약수를 계산한다. 이렇듯 구조적 재귀가 아닌 재귀함수의 계산은 단순히 인자의 패턴만을 보고서 판단할 수 없으며 사용된 인자의 의미를 따져 보아야 한다.

주의: gcd' 함수는 음의 정수에 대해서는 gcd와 다르게 작동한다.

In [53]:
gcd (-42) (-36)

6
In [54]:
gcd' (-42) (-36)

-6

gcd 함수처럼 작동하는 함수는 아래와 같이 정의할 수 있다. (참고: https://wiki.haskell.org/99_questions/Solutions/32)

In [55]:
myGCD x y | x < 0     = myGCD (-x) y
          | y < 0     = myGCD x (-y)
          | y < x     = gcd' y x
          | otherwise = gcd' x y
In [56]:
myGCD (-42) (-36)

6

연습문제

정수 리스트([Integer])에 포함된 항목들의 합(sum), 곱(product), 개수(length)를 계산하는 함수 sum', product', length'을 구조적 재귀함수로 정의하라.

sum' :: [Integer] -> Integer
product' :: [Integer] -> Integer
 length' :: [Integer] -> Integer

주의: sum, product, length 함수는 하스켈의 기본 함수로 이미 정의되어 있다.

In [40]:
sum [1..10]

55
In [43]:
product [1..10]

3628800
In [44]:
length [1..10]

10

5.3 비구조적 재귀(Non-structural Recursion)

앞서 살펴본 gcd' 함수처럼 구조적 함수를 따르지 않는 재귀함수를 좀 더 살펴보자.

시작단계가 없는 재귀: 무한반복 계산

시작단계가 없는 비구조적 재귀 함수를 정의하면 무한반복 계산이 발생할 수 있다. 아래 예제가 무한반복 계산의 위험성과 가능성을 동시에 잘 보여준다.

예제: repeat 함수 구현

repeat 함수는 지정된 인자만을 무한이 많이 포함하는 리스트를 생성한다.

  • 위험성: 아래와 같이 실행하면 무한반복 계산이 발생한다.

    repeat 3

  • 가능성: 예를 들어, 임의의 양의 정수 n에 대해 take n (repeat 3) 은 3을 n 개 갖는 리스트를 반환한다.

In [14]:
take 5 (repeat 3)

[3,3,3,3,3]
In [16]:
take 10 (repeat 3)

[3,3,3,3,3,3,3,3,3,3]

이렇듯 무한 리스트를 생성하는 repeat 함수를 직접 재귀함수로 구현하면 다음과 같다.

주의: 시작단계에 해당하는 패턴이 없다.

In [10]:
repeat' :: a -> [a]
repeat' x = x : repeat' x

예를 들어, repeat' 3을 실행하면 아래의 계산과정을 밟는다.

repeat' 3 = 3 : repeat' 3
          = 3 : 3 : repeat' 3
          = 3 : 3 : 3 : repeat' 3
          = 3 : 3 : 3 : 3 : repeat' 3
          = 3 : 3 : 3 : 3 : 3 : repeat' 3
          = ...
          = [3,3,3,3,3,...]

take 함수를 이용한 결과는 앞서 본 결과와 동일하다.

In [19]:
take 5 (repeat' 3)

[3,3,3,3,3]
In [20]:
take 10 (repeat' 3)

[3,3,3,3,3,3,3,3,3,3]

인자 패턴과 무관한 재귀

함수를 재귀적으로 계산할 때 사용되는 인자가 기존에 주어진 인자의 패턴과 별 상관이 없는 경우를 살펴본다.

예제: 퀵정렬(Quick Sort)

Ord 클래스에 속하는 유형의 값들로 이루어진 리스트의 항목을 오름차순으로 정렬하여 새로운 리스트를 생성하는 퀵정렬 함수 quicksort를 정의해보자. 먼저, 다음이 성립한다.

quicksort :: (Ord a) => [a] -> [a]
  • 시작단계: 비어있는 행렬을 정렬하면 비어있는 행렬이 된다. 
quicksort [] = []

  • 재귀단계: 주어진 리스트의 헤드가 x일 때, 정렬된 리스트는 아래 모양을 갖는다. 조건제시법을 사용하였음에 주의하라.

    (quicksort [a | a <- xs, a <= x]) ++ [x] ++ (quicksort [a | a <- xs, a > x])
    • [a | a <- xs, a <= x]: x 보다 작거나 같은 항목으로 이루어진 리스트
    • [a | a <- xs, a > x]: x 보다 큰 항목으로 이루어진 리스트
    • x: 피벗(pivot) 역할을 수행하며, 여기서는 리스트의 머리(헤드)를 사용함.

재귀단계에서 사용되는 퀵정렬 알고리즘은 다음과 같다.

  • 피벗보다 작거나 같은 항목들은 리스트 왼편에 위치시킨 후 정렬
  • 피벗보다 큰 항목들은 리스트 오른편에 위치시킨 후 정렬
  • 피벗은 정렬된 두 리스트 사이에 위치

즉, 피벗을 선택한 후에 정의된 두 리스트에 대해 재귀가 작동한다. 그런데 사용되는 인자가 애초에 주어진 리스트의 패턴 xs와 형식적인 면에서 별 상관 없으며, 조건제시법으로 정의된 리스트의 의미를 알아야만 퀵정렬의 작동원리를 이해할 수 있다.

재귀적으로 정의된 quicksort 함수는 다음과 같다.

In [30]:
quicksort :: (Ord a) => [a] -> [a]
quicksort []     = []
quicksort (x:xs) =
    let pivot = x
        smallerSorted = quicksort [a | a <- xs, a <= pivot]
        biggerSorted  = quicksort [a | a <- xs, a > pivot]
    in  smallerSorted ++ [pivot] ++ biggerSorted

아래와 같이 잘 작동함을 확인할 수 있다.

In [31]:
quicksort [5,1,9,4,6,7,3]

[1,3,4,5,6,7,9]
In [32]:
quicksort ["edf", "abcd", "vwxyz", "haskell", ";-)"]

[";-)","abcd","edf","haskell","vwxyz"]

예를 들어, quicksort [5,1,9,4,6,7,3]가 계산되는 과정은 아래 그림과 같다.

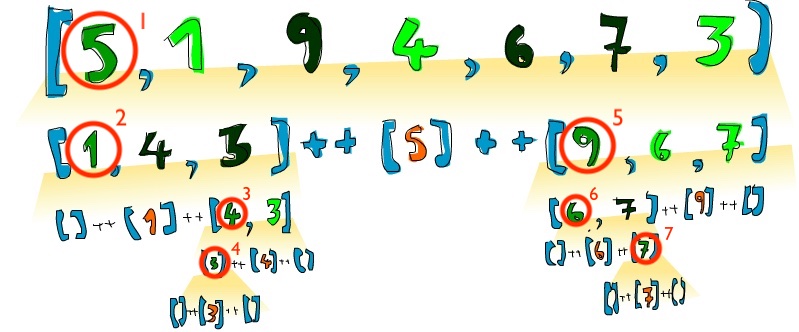
리스트 항목의 각 숫자의 색깔의 의미는 다음과 같다.

  • 초록 숫자: 피벗으로 사용되는 숫자
  • 연초록 숫자: 피벗보다 작거나 같은 숫자
  • 검정 숫자: 피벗보다 큰 숫자

  • 주황 숫자: (피벗으로 선택된 후) 적당한 자리에 위치한 수

  • 연노랑으로 표시된 영역은 quicksort 함수가 실행되는 과정 표시

1부터 6까지의 빨강 숫자는 quicksort 함수가 재귀적으로 사용되는 순서를 가리킨다. 예를 들어, 아래 표현식에서 quicksort [1,4,3]이 먼저 [1,3,4]를 반환할 때까지 quicksort [9,6,7]의 계산은 이루어지지 않는다.

quicksort [1,4,3] ++ [5] ++ quicksort [9,6,7]

위 그림에서 나타낸 계산과정을 요약하면 다음과 같다.

quicksort [5,1,9,4,6,7,3] 
    = quicksort [1,4,3] ++ [5] ++ quicksort [9,6,7]
    = (quicksort [] ++ [1] + [4,3]) ++ [5] ++ quicksort [9,6,7]
    = ...
    = [1,3,4] ++ [5] ++ quicksort [9,6,7]
    = [1,3,4] ++ [5] ++ (quicksort [6,7] + [9] + quicksort [])
    = ...
    = [1,3,4] ++ [5] ++ [6,7,9]
    = [1,3,4,5,6,7,9]

참고: 퀵정렬에 대한 보다 자세한 이해를 위해 YouTube 퀵정렬 설명 동영상을 시청할 것을 권유한다. 피벗(pivot)을 임의로 선정하는 방식을 사용하지만 퀵정렬 알고리즘의 기본 작동방식은 완전히 동일하다. (6분25초 정도까지만 시청해도 됨. 이후엔 자바 언어를 이용한 알고리즘 구현을 설명함.)

5.4 구조적 재귀 대 귀납적 정의

앞서 살펴본 fib 함수의 정의는 구조적 재귀를 따르지 않는다. 이유는 n-1과 n-2 둘 모두 패턴 변수 n의 하위패턴이 아니기 때문이다. 사실 n-1과 n-2가 의미상 n 보다 작은 값을 표현한다는 사실과 n의 하위패턴이라는 것은 서로 별개이다. 그런데 인자를 자연수(음이 아닌 정수)로 제한하면 fib' 함수를 구조적 재귀함수로 정의할 수 있다. 이 점을 여기서 설명한다.

자연수 유형

fib' 함수의 인자를 자연수 유형의 값으로 지정하려면 먼저 Integer 또는 Int 처럼 독립적으로 사용할 수 있는 자연수 유형이 필요하다. 자연수들의 유형은 하스켈의 기본 모듈에 포함되어 있지 않지만 아래와 같이 간단하게 정의할 수 있다.

In [2]:
data Nat = Zero | Succ Nat

위 정의에서 data는 귀납적(inductive)으로 유형을 선언할 때 사용하는 키워드이며, Nat 라는 이름의 유형과 함께 Nat 유형을 갖는 값들을 함께 선언하고 있다. 즉, Nat 유형의 값이 가질 수 있는 패턴은 Zero 또는 Succ n 두 가지이다.

두 패턴이 가리키는 값은 다음과 같다.

  • Zero 패턴: 0에 해당
  • Succ n 패턴: n+1, 즉, 1보다 큰 수에 해당. n은 Nat 유형의 임의의 값을 가리키는 패턴 변수.

Nat 유형의 값이 음이 아닌 모든 정수와 1대1로 연결됨을 쉽게 알 수 있다. 예를 들어, 0, 1, 2, 3, 등 모든 자연수는 아래와 같이 표현된다.

  • 0: Zero
  • 1: Succ Zero
  • 2: Succ (Succ Zero)
  • 3: Succ (Succ (Succ Zero))
  • 4: Succ (Succ (Succ (Succ Zero)))
  • ...

참고: data 키워드 활용법은 나중에 보다 자세히 다룬다.

비록 Succ (Succ (Succ Zero)))를 3 대신에 사용하는 일이 좀 귀찮아 보이기는 하지만 Nat, Zero, Succ 세 기호만을 이용하여 모든 자연수를 다룰 수 있다는 사실은 매우 획기적이다. 여기서 보다 자세히 다루지는 않겠지만, 위 방식으로 모든 연산을 정의하고 수행할 수 있다. 예를 들어, fib' 함수를 다음과 같이 구조적 재귀를 이용하여 정의할 수 있다.

In [3]:
fib' :: Nat -> Integer
fib' Zero            = 0
fib' (Succ Zero)     = 1
fib' (Succ (Succ n)) = fib' (Succ n) + fib' n

시작단계와 재귀단계에 사용된 패턴은 다음과 같다.

  • 시작단계: Zero와 Succ Zero, 즉, 0과 1일 때.
  • 재귀단계: (Succ (Succ n)), 즉, 2 이상일 때. (Succ n)과 n 모두 (Succ (Succ n))의 하위패턴임.

귀납적 정의

Nat와 같이 특정 유형을 귀납적 정의(inductive definition)를 이용하여 선언하려면 해당 유형을 갖는 값(value)을 시작단계와 귀납단계를 이용하여 표현할 수 있어야 한다. 앞서 설명하였듯이 Nat 유형의 값은 모두 Zero 이거나 Succ n 패턴의 표현식으로 표현되어야 한다. 여기서 n 또한 Nat 유형의 값이기에 Nat 유형의 값은 모두 아래와 같이 표현된다(아래 표현식에서 Succ 기호의 사용횟수는 음이 아닌 정수이며, Succ가 0번 사용되었다면 위 표현식은 Zero를 나타낸다).

Succ (Succ (Succ (... (Succ Zero)...)))

귀납적 정의에 사용된 기호들은 사실 함수이다. 예를 들어, Zero는 Nat 유형의 값을 갖는 상수함수이다.

In [4]:
:t Zero
Zero :: Nat

반면에 Succ 기호는 자연수를 인자로 받아 그보다 1만큼 큰 자연수를 계산하는 함수이다.

In [5]:
:t Succ
Succ :: Nat -> Nat

이와 같이 유형의 귀납적 정의에 사용된 기호들을 해당 유형의 생성자(constructor)라고 부르며, 각 생성자는 해당 유형의 값을 생성하는 역할을 수행하는 함수이다. 예를 들어, Zero는 자연수 0을 생성하며, Succ는 하나의 자연수를 이용하여 새로운 자연수를 생성한다. 그리고 그런 방식으로 모든 자연수를 유일한 방식으로 생성할 수 있다. 즉, 어떤 자연수도 Succ와 Zero를 이용하여 표현할 수 있으며, 또한 어떤 특정 자연수를 표현하는 방식은 유일하다.

예제: 이진 트리 유형

아래와 같은 나무 모양의 그래프를 이진 트리(binary tree)라 부른다.

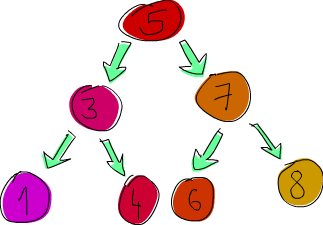
즉, 이진 트리는 하나의 잎으로 구성되었거나, 두 개의 이진트리를 하나의 마디에 연결한 형태를 갖는다. 또한 위 이진 트리 각각의 잎(leaf)와 마디(node)는 하나의 자연수가 위치한다. 이 성질을 귀납적으로 표현하면 아래와 같은 이진 트리 유형인 Tree를 정의할 수 있다.

In [6]:
data Tree = Leaf Nat | Node Nat Tree Tree

Tree 유형의 정의에 사용된 생성자는 Leaf와 Node 두 개이며, 각각의 함수 유형은 다음과 같다.

  • Leaf: 지정된 자연수 인자를 담은 잎 하나로 구성된 이진 트리 생성
In [7]:
:t Leaf
Leaf :: Nat -> Tree
  • Node: 두 개의 이진 트리를 지정된 자연수를 담은 마디로 연결하여 새로운 이진 트리 생성
In [8]:
:t Node
Node :: Nat -> Tree -> Tree -> Tree

위 이미지의 이진 트리에 사용된 잎 네 개에 해당하는 이진 트리는 다음과 같다.

Leaf 1
Leaf 4
Leaf 6
Leaf 7

아래 두 이진 트리에 대한 표현식은 다음과 같다.

Node 3 (Leaf 1) (Leaf 4)
Node 7 (Leaf 6) (Leaf 8)

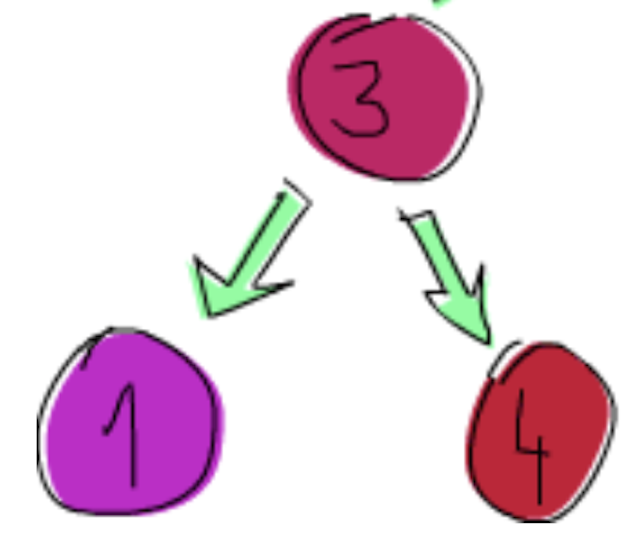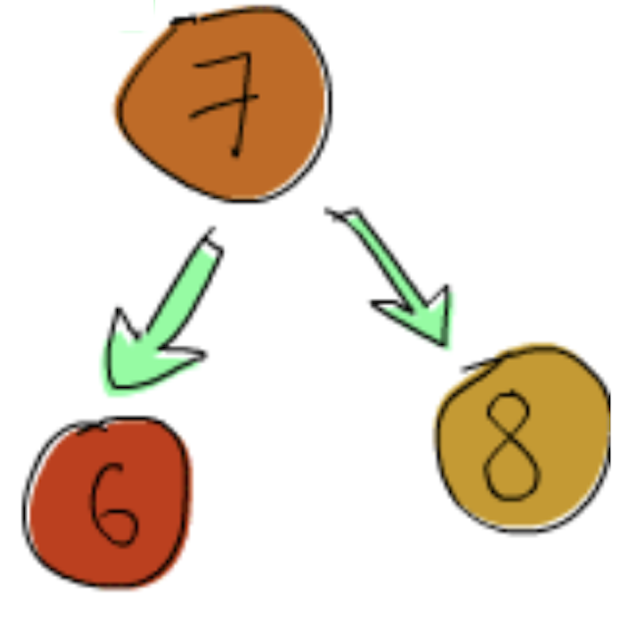따라서 아래 표현식이 애초에 주어졌던 이진 트리를 나타낸다.

Node 5 (Node 3 (Leaf 1) (Leaf 4)) (Node 7 (Leaf 6) (Leaf 8))

귀납적 재귀 다시 이해하기

Nat 와 Tree 를 이용한 재귀함수를 활용하여 두 개념 사이의 관계 설명 필요!!!

In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:

연습문제

예제: replicate 함수 구현

fib' 함수처럼 엄밀하게 따지면 구조적 재귀를 따르지 않지만 인자를 음의 정수로 제한하면 구조적 재귀를 따른다고 볼 수 있는 함수를 좀 더 살펴보자.

먼저, replicate 함수를 직접 구현한다.

replicate takes an Int and some element and returns a list that has several repetitions of the same element. For instance, replicate 3 5 returns [5,5,5]. Let's think about the edge condition. My guess is that the edge condition is 0 or less. If we try to replicate something zero times, it should return an empty list. Also for negative numbers, because it doesn't really make sense.

In [13]:
replicate' :: (Num i, Ord i) => i -> a -> [a]
replicate' n x
    | n <= 0    = []
    | otherwise = x:replicate' (n-1) x

We used guards here instead of patterns because we're testing for a boolean condition. If n is less than or equal to 0, return an empty list. Otherwise return a list that has x as the first element and then x replicated n-1 times as the tail. Eventually, the (n-1) part will cause our function to reach the edge condition.

참고: Num is not a subclass of Ord. That means that what constitutes for a number doesn't really have to adhere to an ordering. So that's why we have to specify both the Num and Ord class constraints when doing addition or subtraction and also comparison.

예제

Next up, we'll implement take. It takes a certain number of elements from a list. For instance, take 3 [5,4,3,2,1] will return [5,4,3]. If we try to take 0 or less elements from a list, we get an empty list. Also if we try to take anything from an empty list, we get an empty list. Notice that those are two edge conditions right there. So let's write that out:

In [14]:
take' :: (Num i, Ord i) => i -> [a] -> [a]
take' n _
    | n <= 0   = []
take' _ []     = []
take' n (x:xs) = x : take' (n-1) xs

The first pattern specifies that if we try to take a 0 or negative number of elements, we get an empty list. Notice that we're using _ to match the list because we don't really care what it is in this case.

Also notice that we use a guard, but without an otherwise part. That means that if n turns out to be more than 0, the matching will fall through to the next pattern. The second pattern indicates that if we try to take anything from an empty list, we get an empty list. The third pattern breaks the list into a head and a tail. And then we state that taking n elements from a list equals a list that has x as the head and then a list that takes n-1 elements from the tail as a tail.

예를 들어, take' 3 [4,3,2,1]이 계산되는 과정은 다음과 같다.

take' 3 [4,3,2,1] = 4 : take' 2 [3,2,1]
                  = 4 : 3 : take' 1 [2,1]
                  = 4 : 3 : 2 : take' 0 [1]
                  = 4 : 3 : 2 : []
                  = [4,3,2]

5.5 재귀함수의 정지문제

정지문제

모든 재귀함수를 항상 구조적 재귀함수로 정의할 수는 없다. 구조적 재귀를 사용하지 않는 재귀함수는 경우에 따라 계산 실행이 언제 멈출지 알 수 없는 경우가 발생하며, 일반적으로 판단이 불가능하다 (튜링의 정지문제 동영상 참조).

잠시 뒤에 콜라츠 추측(Collatz conjecture)을 설명하면서 계산실행이 언젠가는 멈추기는 하지만 얼마나 오래 걸리는지 예측하는 방법은 아직 알려지지 않은 재귀함수를 살펴볼 것이다.

콜라츠 추측

콜라츠 추측(Collatz Conjecture)에서 언급된 함수를 이용하여 구조적 재귀를 사용하지 않는 재귀함수의 정지문제의 판단이 매우 어렵거나 경우에 따라 판단이 불가능할 수 있음을 설명한다.

콜라츠 추측에서 사용된 재귀함수는 다음과 같다.

$$ f(n) = \begin{cases} 1, & n = 1 \\ f(\frac{n}{2}), & n \text{은 짝수} \\ f(3 n + 1), & n \text{은 1보다 큰 홀수} \end{cases} $$

예를 들어, $f(3)$이 계산되는 과정은 다음과 같다.

f(3) => 3*3+1 = 10 
     => 10/2  = 5
     => 3*5+1 = 16
     => 16/2  = 8
     => 8/2   = 4
     => 4/2   = 2
     => 2/2   = 1
     => 1

콜라츠 추측은 함수 $f$가 임의의 양의 정수 $n$에 대해 항상 1을 반환하며 실행을 멈춘다는 내용이다. 하지만 이에 대한 어떠한 증명도 지금까지 알려지지 않았다.

콜라츠 재귀함수의 정지문제

아래 함수는 위 함수 $f$가 각 인자에 대해 재귀적으로 몇 번 호출되는가를 세어주는 함수이며 가드를 활용하여 정의되었다.

In [19]:
collatz :: Integer -> Integer
collatz n
    | n <= 1           = 1
    | (n `mod` 2) == 0 = collatz (n `div` 2) + 1
    | (n `mod` 2) == 1 = collatz (3 * n + 1) + 1

콜라츠 추측에서 주장하듯이 몇 개의 입력값을 사용해 보면 모두 실행이 끝남을 확인할 수 있다. 사실 지금까지 콜라츠 추측이 틀렸음을 입증하는 반례가 알려지지 않았다. 하지만 임의의 수를 입력할 때 실행이 언제 멈출 것인가 또한 앞서 언급한 대로 아직 아무도 모른다.

예를 들어, 3을 인자로 사용하면 8번 먼에 실행을 멈춘다.

In [20]:
collatz 3

8

인자 100에 대해서는 함수 $f$가 26번 호출된다.

In [21]:
collatz 100

26

인자 171에 대해서는 125번 호출된다.

In [22]:
collatz 171

125

1부터 10,000까지를 대상으로 했을 때 함수 $f$가 가장 많이 호출되는 횟수는 다음과 같다.

  • 앞서 언급한 map 함수를 이용하여 1부터 10,000까지의 정수에 collatz 함수를 적용한 후 maximum 함수를 이용하여 최댓값을 찾는다.
In [23]:
collaztNumbers = map collatz [1..10000]
In [24]:
maximum collaztNumbers

262

함수 $f$를 262 번 호출하도록 하는 인자는 Data.List 모듈에 포함된 elemIndices 함수를 이용하여 확인할 수 있다.

  • 모듈 활용법은 나중에 자세히 설명한다. 여기서는 먼저 특정 모듈을 아래와 같이 불러온다(import)는 것만 기억해두면 된다.
In [57]:
import Data.List

이제 262가 위치한 자리의 인덱스는 6170 하나인 것으로 확인된다.

In [26]:
elemIndices 262 collaztNumbers

[6170]

리스트 [1..10000] 에서 6170 인덱스를 갖는 값은 6171이다(인덱스는 0부터 시작하기 때문임). 실제로 6171을 collatz 함수의 인자로 사용하면 262가 반환된다.

In [27]:
collatz 6171

262